Tree

Types of Trees

A tree has a root node in general.
A root node has 0 or more child node.
The child node has also 0 or more child node and it’s defined repeatedly.

A simple definition of a node (GO)

type Node struct {
  name        string
  children    []*Node
}

A simple definition of a tree (GO)

type Tree struct {
  root        *Node
}

General ree

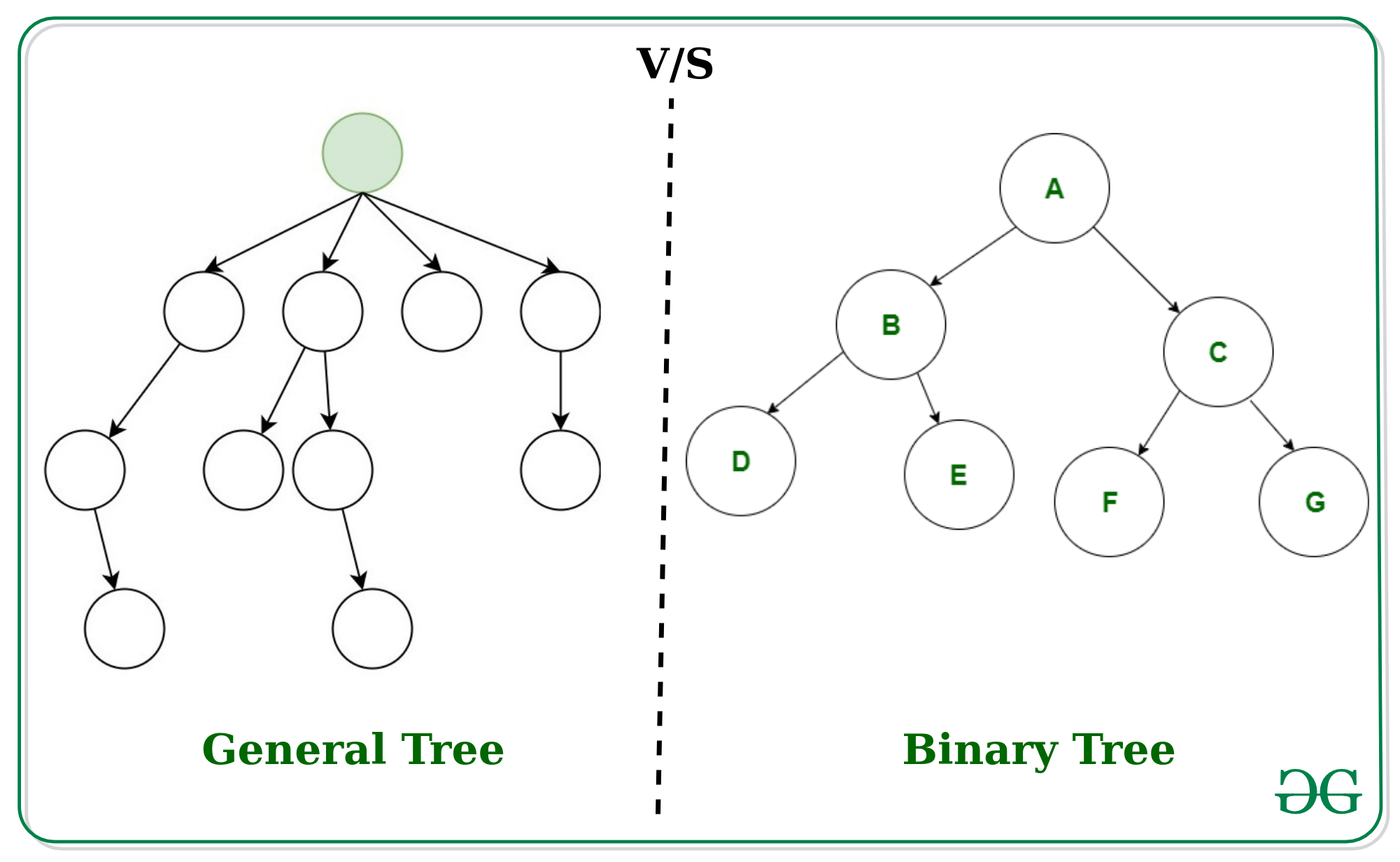
General Tree

No constraint is placed on the tree’s hierarchy.

Binary Tree

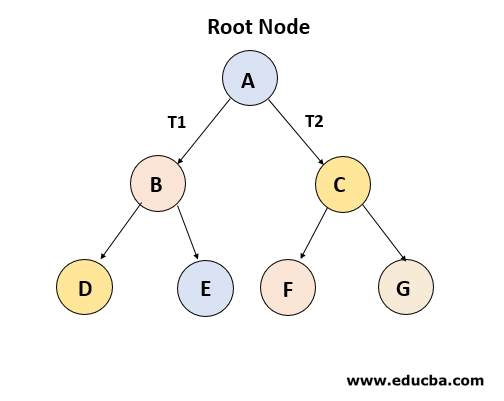
Every node has maximum of two children.

Binary Search Tree

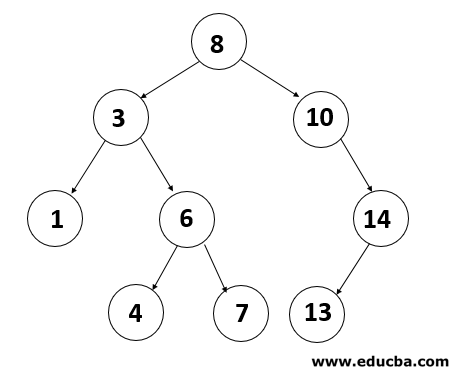
All children on the left <= n < all children on the right

The above property must be true for all nodes n.

Complete Binary Tree

CBT

It is a binary tree whose nodes are full at all heights of the tree.
The last level doesn’t have to be full, but the nodes must be filled from left to right.

Full Binary Tree

FBT

Every node must have exactly 0 or 2 children

Perfect Binary Tree

PBT

The number of nodes : 2^k-1

It is both a balanced tree and full binary tree.
All leaf nodes have the same height, and the number of nodes at the last level is maximum.

Binary Tree Traversal

in-order traversal

visit left branch -> current node -> right branch
func inOrderTraversal(node *TreeNode) {
    if (node != null) {
        inOrderTraversal(node.left)
        visit(node)
        inOrderTraversal(node.right)
    }
}
In the case of a binary search tree, it is visited in ascending order.

pre-order traversal

visit current node -> left branch -> right branch
func preOrderTraversal(node *TreeNode) {
    if (node != null) {
        visit(node)
        inOrderTraversal(node.left)
        inOrderTraversal(node.right)
    }
}
It always visits the root node first.

post-order traversal

visit left branch -> right branch -> current node
func postOrderTraversal(node *TreeNode) {
    if (node != null) {
        inOrderTraversal(node.left)
        inOrderTraversal(node.right)
        visit(node)
    }
}
It always visits the root node last.

장지원